Non è facile capire cosa significhi “crescita esponenziale” se si è abituati all’uso sbrigativo e scorretto che si fa del termine come sinonimo di “crescita grandissima” o “crescita rapidissima”. In matematica esponenziale vuole dire una cosa precisa e diversa da queste: per dire, una crescita esponenziale può essere anche molto piccola e molto lenta, a seconda dei numeri e delle variabili su cui è applicata.
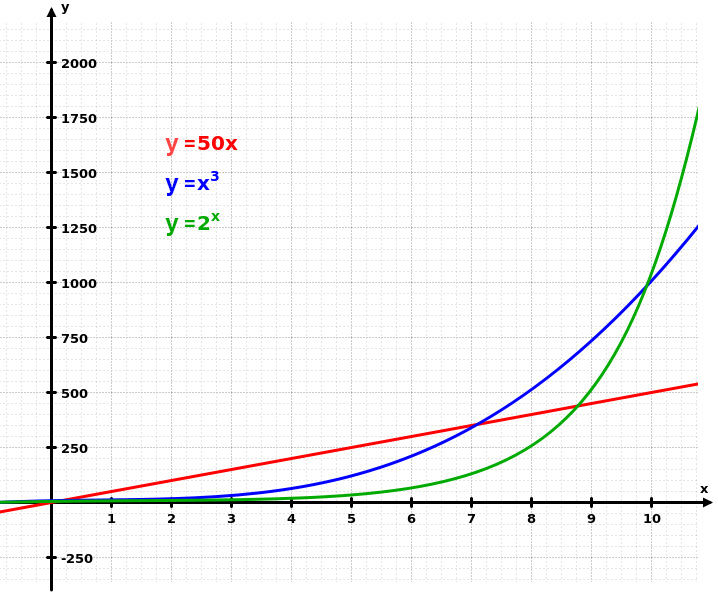
Ma la farò breve, e mi perdoneranno i matematici se semplifico un po’: ci sono grossomodo tre tipi di andamenti di una funzione matematica che ci interessano, rispetto alla realtà, per esempio ai dati che riguardano il coronavirus. Una funzione “lineare” è quando qualcosa aumenta della stessa misura ogni giorno (y=kx). Una funzione “polinomiale” è quando l’aumento stesso invece cresce di giorno in giorno e la crescita dipende da una potenza fissa (o al quadrato, o al cubo, o eccetera). Poi c’è una funzione “esponenziale”, in cui gli aumenti sono legati a una potenza che a sua volta cresce ogni giorno (prima al quadrato, poi al cubo, poi alla quarta, e così via).
Sia nelle funzioni polinomiali che in quelle esponenziali, l’aumento cresce ogni giorno: ma con accelerazioni diverse, che nel caso delle funzioni polinomiali possono essere piccole all’inizio ma diventano presto grandissime. Questi sono esempi possibili dei tre tipi di funzione (la polinomiale blu è in questo caso una “cubica”).
Ora, se si vuole usare queste cose astrattamente matematiche per capire qualcosa della realtà bisogna avere presente una cosa: ovvero che raramente la realtà si dispiega seguendo formule così semplici. Le variabili e i cambiamenti di stato sono tantissimi, per cui i dati reali seguono degli andamenti definiti e continui solo dentro determinati intervalli, spesso brevi. Non c’è, per capirsi, una funzione matematica che descriva la crescita della popolazione mondiale dall’anno zero a oggi: ma ci sono funzioni che si avvicinano abbastanza a descrivere crescite della popolazione su qualche anno, o qualche decennio.
La seconda cosa da dire a premessa del mettere in relazione tutto questo con i dati sul contagio da coronavirus in Italia, è che i dati sul contagio da coronavirus in Italia hanno un valore molto parziale: sia perché non si riferiscono ai reali contagiati, sia perché danno la sensazione di un certo disordine di raccolta e aggregazione. Stiamo ragionando su basi precarie, insomma (il dato più significativo secondo chi segue meglio è quello che riguarda i pazienti in terapia intensiva).
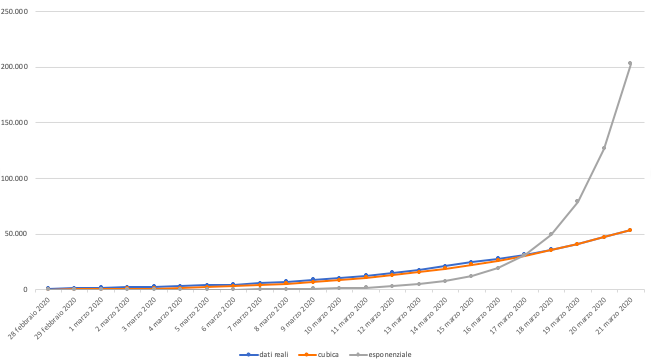
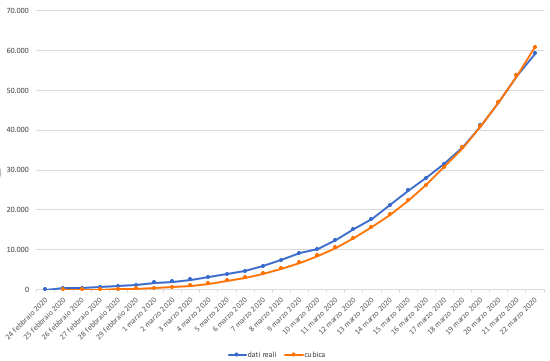
Guardiamo i dati su un grafico, per paragonare appunto funzioni e dati reali. La curva blu corrisponde al numero dei contagi in Italia comunicati ogni giorno dalla Protezione Civile. La curva arancione è una funzione y=x alla 3,342 (non è una cubica, che è y=x alla 3, ma con qualche grossolana approssimazione la chiamerò ora cubica, per capirsi). Non le distinguete benissimo, le curve blu e arancione, perché si sovrappongono molto, e ora ci arriviamo. La terza curva è una curva esponenziale scelta (y=1,6 alla x) tra quelle che avessero un percorso più vicino alla curva azzurra.
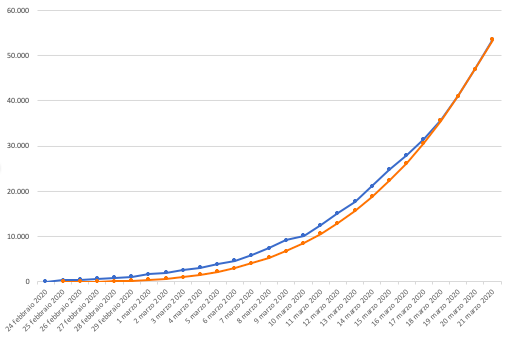
A occhio, sembrano palesi due cose. La prima è che la curva dei contagi non ha mai avuto un intervallo in cui la crescita fosse esattamente esponenziale: ho provato con basi diverse da 1,6 ma lo stesso l’aderenza tra le due curve non si mantiene mai neanche su una coppia sola di giorni. La seconda è che la curva dei contagi si sta fermando negli ultimi giorni su un’aderenza stabile alla cubica, e questa è la ragione per cui l’ho scelta come esempio. Vediamolo in un’altra scala che permette di notare meglio come le due curve si siano avvicinate progressivamente, con un rallentamento dell’aumento dell’aumento dei contagi.
 Venerdì, a partire da questa apparente stabilizzazione della crescita dei contagi (lo ripeto la centesima volta: gli aumenti stanno ancora aumentando, stanno solo aumentando meno e in modo più omogeneo: ma i nuovi contagiati sono ancora ogni giorno più del precedente) ho provato a ipotizzare quanti sarebbero stati i contagiati annunciati nei giorni successivi se la successione avesse mantenuto quell’andamento.
Venerdì, a partire da questa apparente stabilizzazione della crescita dei contagi (lo ripeto la centesima volta: gli aumenti stanno ancora aumentando, stanno solo aumentando meno e in modo più omogeneo: ma i nuovi contagiati sono ancora ogni giorno più del precedente) ho provato a ipotizzare quanti sarebbero stati i contagiati annunciati nei giorni successivi se la successione avesse mantenuto quell’andamento.
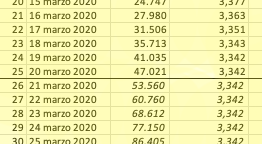
L’ipotesi per sabato, approssimata dall’aver usato solo tre decimali, era di 53.560 contagiati: il numero poi annunciato è stato di 53.578. La curva era quindi rimasta coerente con la cubica (non è una cubica! lo so).
Invece domenica il dato dei nuovi contagiati è persino calato per la prima volta in sei giorni, più basso di sabato e anche di venerdì: è una discontinuità che andrà verificata su un intervallo più lungo, e può avere a che fare con le grosse variabili di incertezza su questi dati, di cui dicevamo (sembra assai più basso il dato della Lombardia). Questo è il grafico aggiornato col dato di sabato, e si vede il discostamento.
Ma spero di avere aiutato a capire di cosa parliamo quando parliamo di crescite e funzioni ed esponenziali.
(ho consultato sei matematici ed epidemiologi per farmi fare le pulci a questa semplificazione – grazie -, ma se dovesse averne bisogno aggiungerò ulteriori integrazioni)
(appunto: alcuni studiosi di queste cose hanno letto il post e mi hanno fatto delle obiezioni non tanto nel merito ma sulla sua stessa esistenza. Tra queste obiezioni quella di cui capisco la fondatezza e l’argomento è che il mio post concorra a suggerire l’idea che ci possano essere dinamiche “facili” di comprensione e prevedibilità del comportamento del virus e della diffusione dei contagi: e che concorra a creare aspettative che rischiano delusioni e reazioni pericolose per tutti. Ho l’impressione di avere sottolineato estesamente la precarietà dei dati in questione e il mio usarli come esempio per spiegare cose più generali e aiutare a renderle più comprensibili quando in giro se ne parla, visto che se ne parla: è un post che parla di matematica usando un’epidemia, non di epidemiologia usando dei numeri. Senza “andare a parare”. Ma capisco e rispetto la preoccupazione e quindi la riporto, ripetendo queste cose)